Fenomeni significativi avvengono quando le distribuzioni di carica e le correnti e, di conseguenza, i campi elettrico e magnetico da queste generati sono quantità variabili nel tempo. Il tipo di variazione temporale di maggior interesse, sia teorico che applicativo, è quello delle oscillazioni periodiche.

Grandezze periodiche

Una grandezza \(a\left(t\right)\), funzione del tempo \(t\), è detta periodica se essa torna ad essere uguale a se stessa dopo un certo intervallo di tempo \(T\), detto periodo. Una quantità correlata con il periodo è la frequenza, \(f\), definita come l’inverso di \(T\), cioè \(f = \frac{1}{T}\). Si può quindi anche dire che la frequenza rappresenta il numero di periodi nell'unità di tempo. Il periodo si misura in secondi e la frequenza si misura in hertz (simbolo, Hz); 1 Hz equivale ad un periodo al secondo.

Una quantità di uso comune per le grandezze periodiche, specie quando si ha a che fare con quantità quali energia o potenza, è il valore efficace. Se \(a\left(t\right)\) è una grandezza periodica, il suo valore efficace \(A\) è definito dalla seguente equazione:

\(A = \sqrt{\frac{1}{T}\int_{T}^{0}a^{2}\left(t\right)dt}\)

Cioè, il valore efficace \(A\) di una data grandezza variabile nel tempo è una quantità il cui quadrato è uguale al valore medio del quadrato di \(a\left(t\right)\).

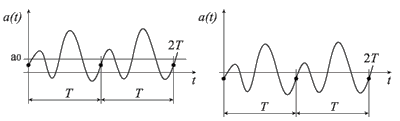
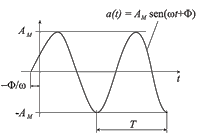
Importanti grandezze periodiche alternate sono le funzioni armoniche sinusoidali e cosinusoidali, così definite:

\(a\left(t\right) = A_{M}\sin\left(\omega t+\phi\right) = A_{M}\cos\left(\omega t+\phi_{1}\right)\) con \(\phi_{1}=\phi-\frac{\pi}{2}\) e dove \(A_{M}=\) ampiezza della funzione armonica; \(\phi =\) fase, \(\phi_{1} =\) fase, \(\omega =2\pi f =\frac{2\pi}{T}\) pulsazione.

Come esempio, si può ricordare che la tensione della rete elettrica ENEL è una grandezza alternata la cui frequenza \(f = 50\,Hz\) e \(T = 20\,millisec\).

Propagazione ondosa

Le variazioni, temporali e spaziali periodiche sono tipiche nei fenomeni ondulatori, comuni in molte manifestazioni naturali, quali le onde sulle superfici libere dei liquidi (es. onde del mare), le oscillazioni di corde e membrane, la propagazione in mezzi elastici (es. onde sonore in gas e aeriformi) o le onde del campo elettromagnetico, di nostro interesse specifico.

Per introdurre alcune definizioni, immaginiamo di osservare la propagazione di una perturbazione ondosa, ad esempio, un’onda sull'acqua. Quel che vediamo è una successione di picchi e di valli che si muovono con regolarità, allontanandosi dal punto in cui l’onda viene prodotta. Il grafico in figura rappresenta una “fotografia” degli spostamenti verticali \(z\) della superficie dell'acqua ad un preciso istante \(t = t_{0}\), in funzione della distanza \(x\) dalla sorgente.

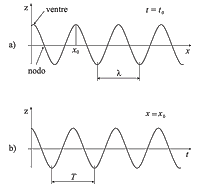I massimi e i minimi della oscillazione sono anche detti, rispettivamente, creste e valli o, più in generale, ventri. La distanza fra due creste successive (oppure fra due valli o due punti successivi di uguale quota e pendenza) è detta lunghezza d’onda ed è comunemente con \(\lambda\). Se invece fissiamo l’attenzione su un particolare punto \(x_{0}\) (mettendo, ad esempio, un galleggiante sulla superficie dell'acqua) e lo osserviamo al passare del tempo, si nota che questo oscilla su e giù con un moto alternativo, senza spostarsi in direzione orizzontale. Ciò che si sposta orizzontalmente è invece la configurazione di massimi e minimi. Questa configurazione trasla lungo \(x\) in modo da percorrere la distanza \(\lambda\) nel tempo \(T\). Per descrivere questo fenomeno, si può dire che l’onda si sposta con velocità \(v\) data dalla espressione seguente: \(v = \frac{\lambda}{T}=\lambda f\)