ENRICOFERMI

Comportamento corpuscolare della radiazione

 

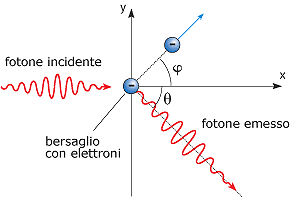
Consideriamo l'effetto scoperto da Arthur H. Compton nel 1923, relativo alla diffusione di un fotone da parte di un atomo. Se ad esempio un sottile fascio di raggi X, di lunghezza d'onda l, attraversa una sostanza di basso peso atomico, da questa si irradiano in tutte le direzioni i raggi X diffusi, che mostrano una lunghezza d'onda diffusa leggermente minore della incidente, seconda la regola:

\[\lambda'-\lambda=0,024\left(1- \cos\varphi\right)\]

Secondo la teoria elettromagnetica classica, quando un raggio di luce (o un raggio X) colpisce gli atomi di un bersaglio, la luce viene diffusa in tutte le direzioni, ma la sua frequenza non cambia. Secondo la teoria dei quanti, invece, la luce è composta di fotoni. Compton pensò che, se i fotoni possono essere pensati come una particella dotata di una quantità di moto, come previsto dalla teoria della relatività, allora nell'urto tra un fotone e un atomo dovrebbe valere la legge della conservazione della quantità di moto.

Compton calcolò la quantità di energia che un fotone dovrebbe perdere nell'urto con un atomo e concluse che non dovrebbe esserci una variazione di energia osservabile se il fotone interagisce con tutto l'atomo, mentre nel caso di un urto contro un singolo elettrone il fotone dovrebbe cedere all'elettrone una quantità di energia considerevole, dato che la massa dell'elettrone è piuttosto piccola [vedi urti].

In alcuni fenomeni come la diffusione, la radiazione elettromagnetica si comporta come se fosse costituita da particelle materiali, mentre in altri esperimenti si comporta come un'onda (diffrazione, interferenza). A questo comportamento si usa dare il nome di dualismo onda-corpuscolo della radiazione.

Comportamento ondulatorio delle particelle

Nel 1923, il fisico francese Louis de Broglie suggerì che il dualismo ondulatorio corpuscolare non si applicasse solo alla radiazione ma anche alla materia, ad esempio agli elettroni e ad altre particelle quantistiche, cioè che fosse una proprietà fondamentale di tutti i processi quantistici. Sviluppando la sua ipotesi, De Broglie trovò un'espressione per la lunghezza d'onda che l'elettrone avrebbe dovuto avere nel suo comportamento ondulatorio. La relazione doveva essere la stessa che lega la quantità di moto di un fotone e la sua lunghezza d'onda. Quindi, la lunghezza d'onda di un elettrone con quantità di moto p = mv deve essere:

\[\lambda=\frac{h}{p}\]

Tale asserzione fu sottoposta a verifica sperimentale, misurando qualcuna delle proprietà ondulatorie dell'elettrone. Questo è stato fatto e il primo effetto ottenuto in laboratorio fu la diffrazione degli elettroni.

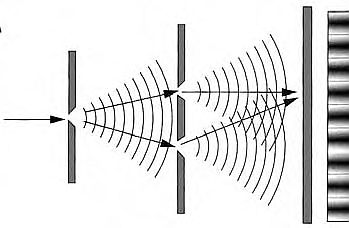
La relazione lunghezza d'onda = h/mv implica che la lunghezza d'onda associata agli elettroni sia molto piccola, anche per elettroni che si muovano molto lentamente; un elettrone accelerato mediante una differenza di potenziale di soli 100 V avrebbe una lunghezza d'onda di appena 10-10 m. Dati gli ordini di grandezza parecchi fisici suggerirono che l'ipotesi di de Broglie potesse essere sottoposta a una verifica usando i cristalli come reticoli di diffrazione per le onde elettroniche. Dagli esperimenti, iniziati nel 1923 da C. J. Davisson e L. H. Germer negli Stati Uniti, si ottennero figure di diffrazione simili a quelle ottenute per i raggi X. La relazione di de Broglie, h/mv, ha una applicazione semplice ma interessante, che parzialmente giustifica il postulato di Bohr, secondo cui per l'elettrone dell'atomo di idrogeno la quantità mvr (chiamata momento della quantità di moto) può assumere solo i valori:

\[mvr=n\frac{h}{2\pi}\] dove n= 1, 2, 3, ...

Supponiamo ora che l'onda dell'elettrone sia in qualche modo distribuita sopra un'orbita di raggio r, cioè che, in un certo senso, essa «occupi» un'orbita di raggio r. La condizione perché un'onda stazionaria si possa stabilire lungo l'orbita è che la lunghezza della circonferenza dell'orbita sia uguale a un numero intero di lunghezze d'onda, cioè:

\[2\pi r=n\lambda\]

Sostituendo la lunghezza d'onda con h/mv, secondo la relazione di de Broglie, otteniamo:

\[mvr=n\frac{h}{2\pi}~~~~~ovvero~~~~2\pi r=n\frac{h}{mv}\]

Ma questa è proprio la condizione di quantizzazione di Bohr! Partendo dalla relazione di de Broglie per le onde associate agli elettroni e facendo l'ipotesi che l'elettrone occupi orbite che permettono lo stabilirsi di onde stazionarie, è possibile ricavare la regola di quantizzazione che Bohr aveva dovuto postulare. Il risultato ottenuto indica che possiamo raffigurare l'elettrone nell'atomo di idrogeno in due modi: come una particella che si muove su di un'orbita con un determinato valore quantizzato di mvr, o come un'onda stazionaria di de Broglie che occupa una certa regione attorno al nucleo.

 Modelli matematici dell'atomo

La prova che «oggetti» (elettroni, atomi, molecole) considerati fino allora come particelle hanno anche proprietà ondulatorie costituì la base per la teoria della struttura atomica attualmente accettata. Questa teoria, la meccanica quantistica, fu introdotta nel 1925; i suoi fondamenti furono sviluppati rapidamente, nel giro di pochi anni, soprattutto da Heisenberg, Born, Schrödinger, Bohr e Dirac.

Schrödinger pensò che le onde di de Broglie, associate con gli elettroni, potessero essere descritte come le onde luminose classiche, cioè che esistesse un'equazione per le onde di materia, così come esiste un'equazione per le onde elettromagnetiche. Egli riuscì in questo modo a dare una espressione matematica della natura duale della materia. La nuova teoria raggiunge le stesse conclusioni della teoria di Bohr senza richiedere nessuna delle ipotesi arbitrarie della teoria precedente, inoltre rende conto anche di alcuni risultati sperimentali che la teoria di Bohr non riusciva a interpretare, come la probabilità di transizione dell'elettrone da un livello energetico a un altro. Il nuovo modello è un modello matematico basato su concetti molto più astratti di quelli su cui poggiava la teoria di Bohr e riesce a interpretare gli eventi e a fare previsioni corrette, fornendo una soluzione per numerosi problemi, ritenuti in precedenza insolubili.

Il principio di indeterminazione

Finora non si è mai messo in dubbio che si possa misurare qualsiasi grandezza fisica con il grado di accuratezza voluto, a patto di possedere uno strumento sufficientemente preciso. La meccanica ondulatoria mostra invece che in esperimenti «ideali», cioè esperimenti in cui si ipotizza l'uso di strumenti perfetti, vi sono limiti alla precisione con cui una misura può essere effettuata. Prendiamo in esame le operazioni necessarie per misurare la velocità e la posizione di un'automobile che si muove lentamente su una strada. Possiamo traguardare la posizione dell'estremità anteriore dell'automobile a un dato istante facendo un segno per terra; contemporaneamente facciamo partire un contasecondi. Poi corriamo alla fine della strada, e nell'istante in cui l'estremità anteriore dell'automobile raggiunge un altro segno sul terreno fermiamo l'orologio. Possiamo quindi ottenere la velocità media dividendo la misura della distanza tra i due segni per la misura del tempo impiegato a percorrerla. In questo modo sappiamo che l'automobile, nell'istante in cui raggiunge il secondo segno, si trova a una certa distanza dal punto di partenza e ha viaggiato a una certa velocità media.

Analizziamo ora in che modo abbiamo ottenuto le informazioni necessarie. Abbiamo determinato la posizione dell'automobile grazie alla luce del sole riflessa dalla parte anteriore dell'automobile verso i nostri occhi. Per determinare la velocità media abbiamo dovuto traguardare l'estremità anteriore due volte. Supponiamo adesso di usare onde radio invece di luce visibile. Alla frequenza di 1000 kHz, tipica dei segnali radio, corrisponde una lunghezza d'onda di 300 m. Con radiazioni di questa lunghezza d'onda, molto maggiore delle dimensioni dell'auto, è impossibile localizzarla con qualsiasi precisione. L'onda verrebbe riflessa o meglio diffusa dall'automobile in tutte le direzioni, proprio come farebbe qualsiasi dispositivo di analoghe dimensioni di cui ci volessimo servire per determinare la direzione dell'onda. Infatti, per determinare la posizione di un oggetto, si deve usare una radiazione di lunghezza d'onda vicina o inferiore alle dimensioni dell'oggetto stesso. Usando onde radar, e cioè con lunghezze d'onda che vanno da 0,1 a 3 cm, l'incertezza nelle misure sarebbe stata di parecchi centimetri; con la luce visibile, la cui lunghezza d'onda è minore di 10-6 m, potremmo invece costruire strumenti così precisi da determinare la posizione dell'automobile con un'accuratezza di pochi millesimi di millimetro.

Consideriamo un elettrone che si muova in un tubo a vuoto. Cercheremo di misurarne posizione e velocità, ma vedremo che per fare ciò è necessario apportare alcuni cambiamenti nei metodi di misura. L'elettrone è talmente piccolo che non è possibile determinarne la posizione usando luce visibile: la lunghezza d'onda nel visibile, pur così piccola, è ancora almeno 104 volte più grande del diametro di un atomo. Per localizzare un elettrone entro una regione di dimensioni atomiche (circa 10-10 m), si deve usare una radiazione di lunghezza d'onda confrontabile con le dimensioni atomiche, preferibilmente minore. Ora un fotone di lunghezza d'onda così piccola possiede una quantità di moto e un'energia molto grandi; abbiamo visto inoltre che durante l'urto, il fotone trasferisce all'elettrone un forte impulso, con il risultato che la sua velocità assumerà una direzione nuova, a noi sconosciuta.

Quindi, dalla direzione del fotone diffuso, possiamo dedurre la posizione in cui si trovava l'elettrone riuscendo così a «localizzarlo», ma dobbiamo tener presente che nel corso del processo di misura abbiamo alterato la velocità dell'elettrone (sia in modulo, sia in direzione). In modo più esplicito: quanto maggiore è la precisione con cui determiniamo la posizione dell'elettrone (usando fotoni di lunghezza d'onda più corta), tanto minore è la precisione con cui ne conosciamo la velocità. Potremmo tentare di perturbare meno l'elettrone impiegando fotoni dotati di energia minore, ma poiché la luce esiste in quanti di energia hn, un fotone di energia minore avrà lunghezza d'onda più grande, e quindi ci darà una indeterminazione maggiore nella misura della posizione dell'elettrone.

Riassumendo: ci troviamo nell'impossibilità di misurare contemporaneamente la posizione e la velocità di un elettrone con precisione illimitata. Questa conclusione è espressa nel principio di indeterminazione, stabilito da Werner Heisenberg.

Il principio di indeterminazione può essere espresso quantitativamente in una semplice formula. Se (delta)x è l'incertezza nella posizione e (delta)p è l'incertezza nella quantità di moto, allora il loro prodotto deve soddisfare la relazione:

\[\Delta x\Delta p \geq \frac{h}{2\pi}\]

dove h è la costante di Planck. Lo stesso ragionamento vale anche per l'esperimento dell'automobile, ma le limitazioni non hanno conseguenze pratiche per un oggetto di massa considerevole.

Interpretazione probabilistica

Le soluzioni dell'equazione di Schrödinger che descrivono il comportamento delle onde associate alle particelle ci danno la probabilità di trovare le particelle in un dato punto a un dato istante. Secondo la moderna teoria quantistica, l'atomo di idrogeno non è formato da una ben precisa particella negativa che si muove attorno a un nucleo, come nel modello di Bohr. Anzi questa teoria non si preoccupa affatto di fornire un modo per visualizzare l'atomo di idrogeno, ma si limita a descrivere la distribuzione di probabilità di occupare una certa zona.

Lo scopo della teoria quantistica non è di determinare la posizione di un singolo elettrone in un singolo atomo, ma piuttosto di fornire un metodo per prevedere l'interazione tra particelle, campi e radiazione. Per esempio, si può calcolare la probabilità che l'idrogeno emetta luce di una particolare lunghezza d'onda, e quindi confrontare i risultati con la distribuzione di intensità e di lunghezze d'onda delle radiazioni emesse da un gran numero di atomi di idrogeno. Esperimenti di questo tipo confermano la teoria.

Oggetto della fisica atomica è il comportamento medio di un gran numero di particelle e le leggi che regolano questo comportamento sono quelle della meccanica ondulatoria. Secondo questa teoria, le onde misurano la probabilità. Le informazioni sulla probabilità (che una determinata particella si trovi in una certa posizione a un dato istante) viaggiano attraverso lo spazio come onde e come tutte le onde possono interferire. Quindi, se, per esempio, un fascio di elettroni attraversa due fenditure, le onde associate agli elettroni danno una figura di interferenza, nella quale i massimi di intensità corrispondono alla massima probabilità di trovare l'elettrone in quel punto. Invece, in assenza di fenditure o comunque di altre interazioni delle onde elettromagnetiche con la materia, possiamo ritornare alla descrizione degli elettroni in termini di particelle e dire che probabilmente essi si muoveranno in una certa direzione e con una certa velocità (e ciò sarà vero per la media degli elettroni).

Malgrado il successo che ebbe l'interpretazione dell'onda come probabilità di trovare la particella ad essa associata in qualche specifica condizione di moto, molti scienziati trovarono difficile accettare l'idea che non si potessero avere informazioni precise sul moto di ciascuna particella. Il più autorevole di questi fu Einstein che, in una lettera a Born del 1926, scriveva: La meccanica quantistica è degna di ogni rispetto, ma una voce interiore mi dice che non è ancora la soluzione giusta. É una teoria che ci dice molte cose, ma non ci fa penetrare più a fondo il segreto del gran Vecchio. In ogni caso sono convinto che questi non gioca a dadi con il mondo.

Eppure, malgrado il rifiuto di Einstein (e di qualche altro scienziato) di accettare le leggi di probabilità in meccanica, nessun fisico è finora riuscito a sostituire l'interpretazione di Born della meccanica quantistica.